درخت پوشا و معرفی الگوریتم های Kruskal و Prim — به زبان ساده
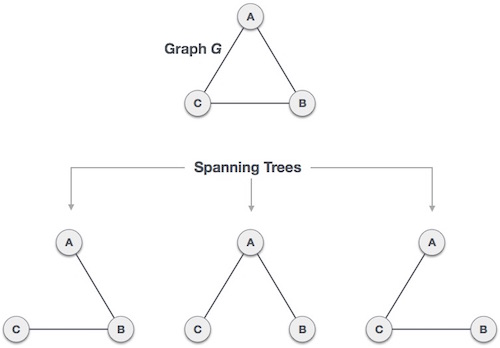
درخت پوشا زیرمجموعهای از گراف G است که همه رئوس آن با کمترین مقدار یالهای ممکن پوشش یافته است. از این رو یک درخت پوشا دور ندارد و هیچ رأس ناهمبندی در آن دیده نمیشود.
بر اساس تعریف فوق میتوانیم نتیجه بگیریم که هر گراف کاملاً همبند و غیر جهتدار G دستکم یک درخت پوشا دارد. یک گراف ناهمبند؛ هیچ درخت پوشایی ندارد، چون امکان پوشش همه رئوس آن میسر نیست.
درختهای پوشای فوق را در یک گراف کامل میتوان یافت. یک گراف کامل غیر جهتدار میتواند بیشینه nn-2 درخت پوشا داشته باشد که n تعداد گرههای آن است. در نمونه فوق n برابر با 3 است و از این رو 33−2 = 3 درخت پوشا میتوان در آن یافت.
مشخصات کلی درخت پوشا
اینک که دانستیم یک گراف میتواند بیش از یک درخت پوشا داشته باشد. در ادامه چند مورد از مشخصات درخت پوشای همبند با درخت G را بررسی میکنیم:
- یک گراف همبند G میتواند بیش از یک درخت پوشا داشته باشد.
- همه درختهای پوشای گراف G تعداد یکسانی از یالها و رئوس را دارند.
- درخت پوشا هیچ دوری ندارد.
- با حذف یک یال از درخت پوشا، به گراف غیر همبند تبدیل میشود، یعنی درخت پوشا دارای کمینه اتصالهای ممکن است.
- افزودن یک یال به درخت پوشا موجب ایجاد یک مدار یا طوقه میشود، یعنی درخت پوشا در حالت بیشینه غیر دوری (maximally acyclic) است.
مشخصات ریاضیاتی درخت پوشا
- درخت پوشا n-1 یال دارد که n تعداد گرهها (رأسها) ی آن است.
- با حذف e-n+1 یال از یک گراف کامل میتوانیم یک درخت پوشا بسازیم.
- یک گراف کامل میتواند در بیشینه حالت خود nn-2 عدد درخت پوشا داشته باشد.
از این رو میتوانیم نتیجه بگیریم که درختهای پوشا زیرمجموعهی از گراف همبند G هستند و گرافهای ناهمبند، درخت پوشا ندارند.
کاربرد درخت پوشا
درخت پوشا اساساً برای یافتن کوتاهترین مسیر بین همه گرهها در یک گراف مورد استفاده قرار میگیرد. کاربردهای رایج درختهای پوشا به صورت زیر هستند:
- برنامهریزی شبکه تأسیسات شهری
- پروتکل مسیریابی شبکه رایانهای
- تحلیل خوشه
با مثال کوچکی کاربردهای درخت پوشا را بررسی میکنیم. شبکه یک شهر را به صورت یک گراف بزرگ تصور کنید. اینک میخواهیم خطوط تلفن را به روشی توزیع کنیم که با کمترین مقدار سیم بتوان همه گرههای شهر را به شبکه وصل کرد. این همان جایی است که درخت پوشا وارد عمل میشود.
درخت پوشای کمینه (MST)
در یک گراف وزندار، درخت پوشای کمینه، آن درخت پوشایی است که کمترین وزن را نسبت به دیگر درختهای پوشای همان گراف داشته باشد. در موقعیتهای دنیای واقعی این وزن میتواند بر اساس مسافت، ازدحام، بار ترافیکی، یا هر مقدار دلخواهی که به یالها اختصاص مییابد اندازهگیری شود.
الگوریتم درخت پوشای کمینه
دو مورد از مهمترین الگوریتمهای درخت پوشای کمینه به صورت زیر هستند:
- الگوریتم کروسکال
- الگوریتم پریم
هر دو این الگوریتمها در دسته الگوریتمهای حریصانه قرار میگیرند که در ادامه هر یک را به تفصیل بررسی میکنیم:
الگوریتم درخت پوشای کمینه کروسکال (kruskal)
الگوریتم کروسکال برای یافتن درخت پوشای با کمترین هزینه از رویکرد حریصانه بهره میگیرد. این الگوریتم با گراف به صورت یک جنگل برخورد میکند که در آن هر گره یک درخت منفرد محسوب میشود. یک درخت زمانی به درخت دیگر وصل میشود اگر و فقط اگر در میان همه گزینههای موجود، کمترین هزینه را داشته باشد و مشخصات درخت پوشای کمینه (MST) را نیز نقض نکند.
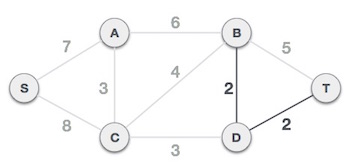
برای درک الگوریتم کروسکال، مثال زیر را در نظر بگیرید:
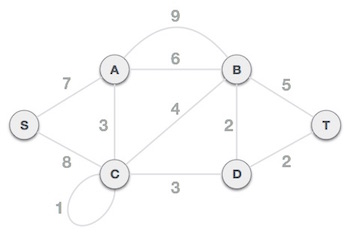
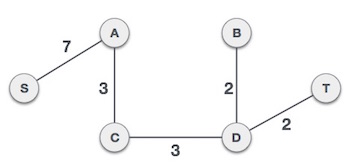
گام 1 – حذف همه یالهای طوقه و موازی
همه یالهای طوقه و یالهای موازی را از گراف فوق حذف میکنیم.
در مورد یالهای موازی، آن یالی را نگه میداریم که کمترین هزینه را دارد و بقیه را حذف میکنیم.
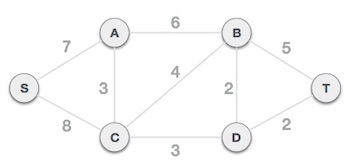
گام 2 – چیدمان همه یالها به ترتیب افزایش وزن
در این مرحله مجموعهای از یالها و وزنهایشان ایجاد میکنیم و آنها را بر اساس ترتیب افزایش وزن (هزینه) میچینیم.
گام 3 – یالی که کمترین وزن را دارد اضافه میکنیم
اینک برای افزودن یالها به گراف، کار خود را از یالی آغاز میکنیم که کمترین وزن را دارد. در تمام طول این فرایند بررسی میکنیم که مشخصات پوشا بودن همچنان برقرار باشد. در موردی که با افزودن یک یال مشخصات درخت پوشا نقض شود، نمیبایست این یال را وارد گراف کنیم.
کمترین هزینه 2 است و یالهای مربوط به آن B,D و D,T هستند. آنها را به گراف اضافه میکنیم. با افزودن این دو یال، مشخصات درخت پوشا نقض نمیشود، بنابراین کار خود را ادامه داده و یالهای بعدی را انتخاب میکنیم. در مرحله بعد هزینه 3 است و یالهای مربوطه A,C و C,D هستند. آنها را نیز اضافه میکنیم.
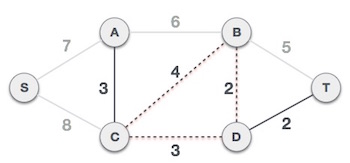
هزینه بعدی در جدول، 4 است و میبینیم که با افزودن یال مربوط به این وزن، یک مدار در گراف ایجاد میشود.
این یال را نادیده میگیریم، چون قرار است در این فرایند همه یالهایی که باعث ایجاد مدار در گراف میشوند را نادیده بگیریم.
اینک مشاهده میکنیم که یالهای مربوط به وزنهای 5 و 6 نیز مدار ایجاد میکنند و آنها را نیز نادیده گرفته و به کار خود ادامه میدهیم:
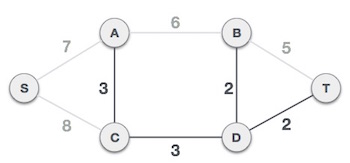
در این زمان تنها یک گره مانده است که باید اضافه شود. بین دو یال با کمترین هزینه 7 و 8 میبایست یالی که وزن 7 دارد را اضافه کنیم.
با افزودن یال S,A همه گرهها در گراف شامل شدهاند و اینک درخت پوشای با کمترین هزینه را داریم.
الگوریتم درخت پوشای پریم (Prim)
الگوریتم پریم برای یافتن درخت پوشای با کمترین هزینه (همانند الگوریتم کروسکال که در بخش قبل بررسی کردیم) از رویکرد حریصانه بهره میگیرد. الگوریتم پریم شباهتهایی با الگوریتمهای «کوتاهترین مسیر، اول» (shortest path first) دارد.
الگوریتم پریم در تضاد با الگوریتم کروسکال است، چون با گرهها به عنوان یک درخت منفرد برخورد میکند و به افزودن گرهها به یک درخت پوشا از گراف مفروض ادامه میدهد.
برای درک این تضاد با الگوریتم کروسکال و برای این که بتوانیم الگوریتم پریم را به خوبی درک کنیم از همان مثال بخش قبلی استفاده میکنیم.
گام 1 – حذف همه یالهای طوقه و موازی
همه یالهای طوقه و همچنین یالهای موازی را از گراف مفروض حذف میکنیم. در مورد یالهای موازی، یالهایی را حفظ میکنیم که کمترین هزینه را دارند و بقیه را حذف میکنیم.
گام 2 – یک گره دلخواه را به عنوان ریشه انتخاب کنید
در این مورد ما گره S را به عنوان گره ریشه درخت پوشای پریم در نظر میگیریم. این گره به طور دلخواه انتخاب شده است و هر گره دیگری به جای آن میتوان انتخاب کرد. ممکن است تعجب کنید که چطور ممکن است هر گرهی به عنوان گره ریشه انتخاب شود، پاسخ این است که در درخت پوشا، همه گرهها در یک گراف گنجانده میشوند و از آن جا که گراف، همبند است، در این صورت میبایست دستکم یک یال برای هر گره باشد که آن را به بقیه درخت متصل سازد.
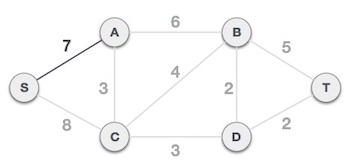
گام 3 – بررسی یالهای خروجی و انتخاب یالی که کمترین هزینه را دارد.
پس از انتخاب گره S به عنوان ریشه میبینیم که یال S,A و S,C دو یالی هستند که به ترتیب وزنهای 7 و 8 دارند. یال S,A انتخاب میشود چون کوچکتر از یال دیگر است.
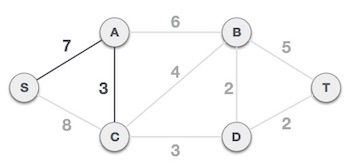
اینک با درخت S-7-A به صورت یک گره رفتار میشود و همه یالهایی که از آن خارج میشوند را بررسی میکنیم. یالی را انتخاب میکنیم که کمترین هزینه را دارد و آن را در درخت میگنجانیم.
پس از این مرحله، درخت S-7-A-3-C تشکیل مییابد. اینک بار دیگر با آن به صورت یک گره برخورد میکنیم و همه یالها را مجدداً بررسی میکنیم. با این حال، مجدداً تنها یالی که کمترین هزینه را دارد انتخاب میکنیم. در این مورد، C-3-D یک یال جدید است که هزینه آن کمتر از یالهای دیگر است.
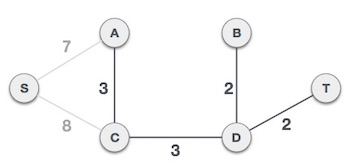
پس از افزودن گره D به درخت پوشا اینک دو یال داریم که از آن خارج میشوند و هزینه یکسانی دارند، یعنی D-2-T و D-2-B. بنابراین میتوانیم هر یک از آنها را که میخواهیم به درخت اضافه کنیم. اما در مرحله بعد یال 2 کمترین هزینه را دارد. از این رو یک درخت پوشا را با گنجاندن هر دو یال نشان میدهیم.
بدین ترتیب درمییابیم که خروجی درخت پوشای گراف با استفاده از هر دو الگوریتم یکسان خواهد بود.
اگر به این نوشته علاقهمند بودید، موارد زیر نیز احتمالاً مورد توجه شما قرار خواهند گرفت:
- آموزش درخت در نظریه گراف و کاربردها
- مجموعه آموزشهای مهندسی نرم افزار
- معرفی الگوریتم های مجانبی، حریصانه و برنامه نویسی دینامیک — به زبان ساده
- ساختمان داده (Data Structure) — راهنمای جامع و کاربردی
- همه چیز در مورد درخت تصمیم (Decision Tree)
- ۳۰ پرسش و پاسخ دربارهی مدلهای درختی
- مجموعه آموزشهای علوم کامپیوتر