گراف و یال

تعاریف و اصطلاحات

همان‌طور که گفتیم، یک گراف، نموداری از نقاط، و خطوطی است که آن‌ها را به یک‌دیگر متصل کرده است. مفهوم گراف‌‌‌ها در نظریه گراف، براساس اصطلاحاتی مانند نقطه، خط، رأس، یال، مرتبه رئوس، ویژگی‌های گراف و... بنا شده است. در ادامه، برخی از این اصطلاحات را توضیح می‌دهیم.

فیلم آموزش نظریه گراف و کاربردها در فرادرس

کلیک کنید

نقطه

نقطه، یک موقعیت خاص در فضای یک‌بعدی، دوبعدی یا سه‌بعدی است. برای درک بهتر، یک نقطه را می‌توان با یک نقطه (همان چیزی که در مکالمات روزمره به کار می‌بریم) توپر نمایش داد و یکی از حروف الفبا را با آن متناظر کرد. برای مثال، نقطه زیر با نام «a» مشخص شده است.

خط

یک خط، ارتباط بین دو نقطه است. خط را با یک خط ممتد نشان می‌دهند. در شکل زیر، «a» و «b» نقطه‌ها هستند. ارتباط بین این دو نقطه یک خط نامیده می‌شود.

رأس

یک رأس، نقطه‌ای است که در آن، چند خط به هم می‌رسند. رأس، گره نیز نامیده می‌شود. مشابه نقاط، رأس را نیز می‌توان با یکی از حروف الفبا نام‌گذاری کرد.

یال

یال، اصطلاحی ریاضی است که برای خطی به‌کار می‌رود که دو رأس را به یک‌دیگر وصل می‌کند. از یک رأس ممکن است تعداد زیادی یال شکل بگیرد. بدون وجود رأس، یالی هم وجود نخواهد داشت. برای هر یال، یک رأس ابتدا و یک رأس انتها وجود دارد. در شکل زیر، دو رأس «a» و «b»، و ارتباط بین آن‌ها، یعنی یال نشان داده شده است.

گراف

گراف G را به‌صورت (G=(V,E تعریف می‌کنیم که در آن، V مجموعه‌‌ای از همه رئوس و E مجموعه همه یال‌های آن است.

مثال ۱

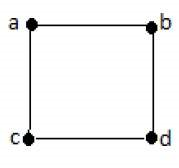
در شکل زیر، cd ،ac ،ab و bd یال‌های گراف هستند. به‌طور مشابه، c ،b ،a و d رئوس گراف را نشان می‌دهند.

مثال ۲

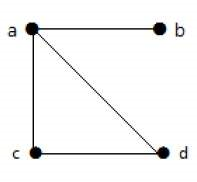
در گراف شکل زیر نیز، c ،b ،a و d رئوس و ad ،ac ،ab و cd یال‌ها را نشان می‌دهند.

حلقه

اگر در یک گراف، یک یال از رأسی شروع و به همان ختم شود، آن را حلقه می‌نامیم.

مثال ۱

در گراف شکل زیر، V یک یال برای رئوس یا رأس (V,V) است که یک حلقه را تشکیل می‌دهد.

مثال ۲

گراف زیر، دو حلقه دارد که در دو رأس a و b تشکیل شده‌اند.

مرتبه یا درجه رأس

تعداد رأس‌های مجاور رأس V را مرتبه یا درجه رأس V می‌نامند و آن را با (deg(V نشان می‌دهند. در یک گراف ساده با n رأس، مرتبه هر کدام از رأس‌ها در رابطه زیر صدق می‌کند:

deg(v) ≤ n – 1

هر رأس می‌تواند با رئوس مجاور یال تشکیل دهد، اما با خودش نمی‌تواند. بنابراین، مرتبه هر رأس، حداکثر برابر با تعداد یال‌های گراف منهای یک است. این عدد ۱، برای نشان دادن این است که رأس مورد نظر نمی‌تواند حلقه تشکیل دهد. اگر یک حلقه در هر یک از رئوس وجود داشته باشد، آن‌گاه گراف ساده نیست. گراف ساده را در ادامه توضیح خواهیم داد.

مرتبه رأس را می‌توان در دو نوع گراف بررسی کرد:

• گراف جهت‌دار
• گراف بدون جهت

مرتبه رأس در گراف بدون جهت

گراف بدون جهت، گرافی است که یال‌های آن جهت ندارند.

مثال ۱

گراف زیر، یک گراف بدون جهت است.

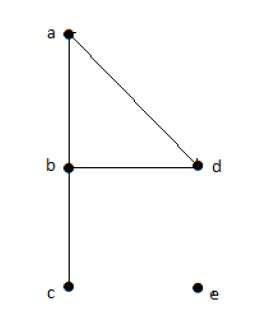
در گراف بالا، مرتبه رئوس به‌شرح زیر است:

• deg(a) = 2، زیرا رأس «a» دو یال دارد.
• deg(b) = ۳، زیرا رأس «b» سه یال دارد.
• deg(c) = 1، زیرا رأس «c» یک یال دارد. بنابراین، «c» یک رأس آویزان است.
• deg(d) = 2، زیرا رأس «d»، دو یال دارد.
• deg(e) = 0، زیرا رأس «e»، هیچ یالی ندارد. بنابراین، «e» یک رأس جدا است.

مثال ۲

گراف شکل زیر را در نظر بگیرید.

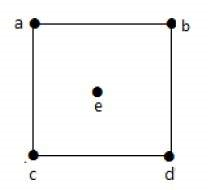
در گراف بالا، داریم:

deg(a) = 2, deg(b) = 2, deg(c) = 2, deg(d) = 2, deg(e) = 0

رأس «e»، یک رأس جدا است. این گراف هیچ رأس آویزانی ندارد.

مرتبه رأس در گراف جهت‌دار

در یک گراف جهت‌دار، هر رأس، یک مرتبه ورودی و یک مرتبه خروجی دارد.

مرتبه ورودی گراف جهت‌دار

مرتبه ورودی رأس V، تعداد یال‌هایی است که به رأس V وارد می‌شوند و آن را با (deg−(V نشان می‌دهند.

مرتبه خروجی گراف جهت‌دار

مرتبه خروجی رأس V، تعداد یال‌هایی است که از رأس V خارج شده که با (deg+(V نشان داده می‌شود.

مثال ۱

گراف جهت‌دار شکل زیر را در نظر بگیرید. دو یال «ad» و «ab» از رأس «a» خارج می‌شوند. بنابراین، مرتبه خروجی آن، برابر با ۲ است. همچنین یال «ga» به این رأس وارد می‌شود. در نتیجه مرتبه ورودی رأس «a»، برابر با ۱ است.

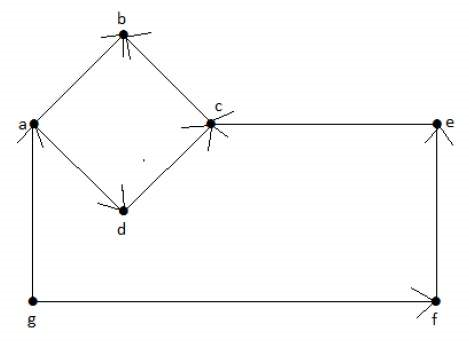
مرتبه ورودی و خروجی سایر رئوس گراف، در جدول زیر آورده شده‌اند.

رأس	مرتبه ورودی	مرتبه خروجی
a	1	2
b	2	0
c	2	1
d	1	1
e	1	1
f	1	1
g	0	2

مثال ۲

گراف جهت‌دار شکل زیر را در نظر بگیرید. در این گراف، یال «ae»‌ از رأس «a» خارج می‌شود. بنابراین، مرتبه خروجی آن برابر ۱ است. به‌طور مشابه،‌ یال «ba» به رأس «a» وارد می‌شود، در نتیجه مرتبه خروجی این رأس برابر با ۱ خواهد بود.

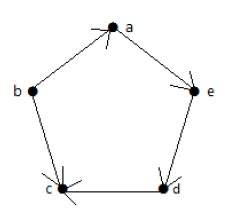
مرتبه ورودی و خروجی سایر رئوس گراف، در جدول زیر آورده شده‌ است.

رأس	مرتبه ورودی	مرتبه خروجی
a	1	1
b	0	2
c	2	0
d	1	1
e	1	1

رأس آویزان

رأسی با یک یال را یک رأس آویزان می‌نامیم. در حقیقت، رأسی آویزان است که مرتبه آن، یک باشد.

مثال

در شکل زیر، رئوس «a» و «b»، از طریق یال «ab» با یک‌دیگر ارتباط دارند. بدیهی است که رأس «a» فقط با رأس «b» ارتباط دارد و بالعکس، بنابراین، رئوس «a» و «b» آویزان هستند.

رأس جدا

رأسی را جدا می‌نامیم که مرتبه آن صفر باشد.

مثال

در شکل زیر، هیچ ارتباطی بین دو رأس «a» و «b» وجود ندارد. بنابراین، مرتبه هردو رأس، صفر است. این رئوس، جدا نامیده می‌شوند.

مجاورت

مجاورت برای رأس و یال به‌صورت زیر تعریف می‌شود:

• در یک گراف، دو رأس را مجاور می‌گوییم، اگر یک یال بین آن‌ها وجود داشته باشد. در این‌جا، مجاورت رئوس با یال متصل‌کننده آن‌ها تعریف می‌شود.
• در یک گراف، دو یال را مجاور می‌گوییم، اگر یک رأس مشترک بین آن‌ها وجود داشته باشد. در این‌جا، مجاورت یال‌ها با رأس مشترک‌شان تعریف می‌شود.

مثال ۱

درباره گراف شکل زیر می‌توان گفت:

• رئوس «a» و «b» مجاور هستند، زیرا یال مشترک «ab» بین آن‌ها وجود دارد.
• رئوس «a» و «d» مجاور هستند، زیرا یال مشترک «ad» بین آن‌ها وجود دارد.
• یال‌های «ab» و «be» مجاور هستند، زیرا رأس مشترک «b» بین آن‌ها وجود دارد.
• یال‌های «be» و «de» مجاور هستند، زیرا رأس مشترک «e» بین آن‌ها وجود دارد.

مثال ۲

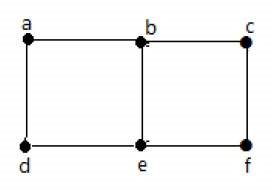
درباره گراف شکل زیر می‌توان گفت:

• رئوس «a» و «d» مجاور هستند، زیرا یال مشترک «ad» بین آن‌ها وجود دارد.
• رئوس «c» و «b» مجاور هستند، زیرا یال مشترک «cb» بین آن‌ها وجود دارد.
• یال‌های «ad» و «cd» مجاور هستند، زیرا رأس مشترک «d» بین آن‌ها وجود دارد.
• یال‌های «ac» و «cd» مجاور هستند، زیرا رأس مشترک «c» بین آن‌ها وجود دارد.

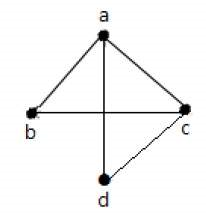
یال‌های موازی

اگر دو رأس یک گراف، با بیش از یک یال به یک‌دیگر وصل شده باشند، آن یال‌ها را یال‌های موازی می‌نامیم.

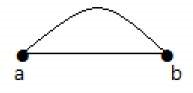
در گراف بالا، «a» و «b»، دو رأس هستند که از طریق دو یال «ab» و «ab» به یک‌دیگر متصل شده‌اند. بنابراین، دو یال موازی هستند.

گراف چندگانه

گرافی که یال موازی داشته باشد، گراف چندگانه یا شبه‌گراف نامیده می‌شود.

مثال ۱

در گراف شکل زیر، پنج یال «cd» ،«cd» ،«ac» ،«ab» و «bd» وجود دارد. از آن‌جایی که بین دو رأس «c» و «d»، دو یال موازی وجود دارد، گراف چندگانه است.

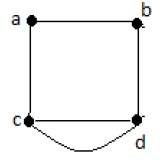
مثال ۲

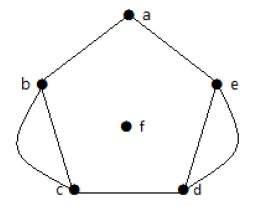
در گراف شکل زیر، بین دو رأس «b» و «c» دو یال وجود دارد. رئوس «e» و «d» نیز دو یال دارند. بنابراین، گراف زیر، یک گراف چندگانه است.

دنباله مرتبه گراف

اگر مرتبه همه رئوس یک گراف را به‌صورت نزولی یا صعودی مرتب کنیم، آن‌گاه این دنباله مرتبه‌ها، به‌عنوان دنباله مرتبه گراف شناخته می‌شود.

مثال ۱

در گراف شکل زیر، برای رئوس {d, a, b, c, e}، دنباله مرتبه، به‌صورت {1 ,2 ,2 ,2 ,3} است.

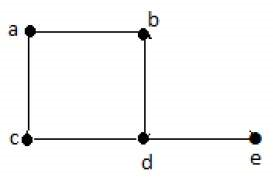
رأس	a	b	c	d	e
متصل به	b,c	a,d	a,d	c,b,e	d
درجه	2	2	2	۳	۱

مثال ۲

در گراف شکل زیر، برای رئوس {a, b, c, d, e, f}، دنباله مرتبه، به‌صورت {0 ,2 ,2 ,2 ,2 ,2} است.

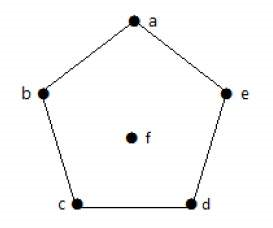
رأس	a	b	c	d	e	f
متصل به	b,e	a,c	b,d	c,e	a,d	-
درجه	2	2	2	2	2	0

مسیر

مسیر، دنباله ای از رأس‌ها است، به‌طوری که از هر أس به رأس دیگرِ این دنباله، یالی وجود داشته باشد.

دور

به مسیری که رأس ابتدایی و انتهایی آن بر هم منطبق باشد، دور می‌گوییم.

ویژگی‌های اساسی گراف‌ها

گراف‌ها ویژگی‌های مختلفی دارند که بسته به ساختارشان می‌توان آن‌ها را مشخص کرد. این ویژگی‌ها با اصطلاحات خاصی بیان می‌شوند که در نظریه گراف تعریف شده است. در ادامه، برخی از ویژگی‌های اساسی گراف‌ها را بیان می‌کنیم.

فیلم آموزش گراف ها و گروه ها در فرادرس

کلیک کنید

فاصله بین دو رأس

فاصله بین دو رأس U و V، تعداد یال‌های کوتاه‌ترین مسیر بین آن‌ها است. این بدین معنی است که اگر چند مسیر بین دو رأس وجود داشته باشد، آن‌گاه کوتاه‌ترین مسیر را برای فاصله بین دو رأس در نظر می‌گیریم. فاصله بین دو رأس U و V‌ را با (d(U,V نشان می‌دهند.

مثال

گراف شکل زیر را در نظر بگیرید.

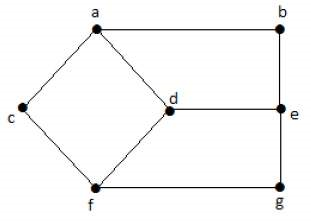
در این گراف، فاصله رأس «d» از رأس «e» برابر با ۱ است، زیرا یک یال بین آن‌ها وجود دارد. مسیرهای بین دو رأس «d» و «e» عبارتند از:

• ab ،da و be
• fg ،df و ge
• de (فاصله بین دو رأس)
• ab ،ca ،fc ،df و be
• fg ،cf ،ac ،da و ge

خروج از مرکز یک رأس

حداکثر فاصله بین یک رأس از رأس‌های دیگر، خروج از مرکز آن رأس نامیده می‌شود. خروج از مرکز رأس V را با (e(V نشان می‌دهند.

مثال

در گراف شکل زیر، خروج از مرکز رأس «a» برابر با ۳ است.

• فاصله «a» تا «b» برابر با ۱ است («ab»).
• فاصله «a» تا «c» برابر با ۱ است («ac»).
• فاصله «a» از «d» برابر با ۱ است («ad»).
• فاصله «a» از «e» برابر با ۲ است («be» ،«ab» یا «de» ،«ad»).
• فاصله «a» از «f» برابر با ۲ است («cf» ،«ac» یا «df» ،«ad»).
• فاصله «a» از «g» برابر با ۳ است («fg» ،«cf» ،«ac» یا «fg» ،«df» ،«ad»).

بنابراین، خروج از مرکز برابر با ۳، یعنی حداکثر فاصله رأس «a» از رأس «g» است.

به عبارت دیگر:

e(g) = 3, e(f) = 3, e(e) = 3, e(d) = 2, e(c) = 3, e(b) = 3

شعاع گراف

کوچک‌ترین خروج از مرکز رئوس گراف G را شعاع گراف می‌نامند و آن را با (r(G نشان می‌دهند.

مثال

در گراف شکل زیر، r(G) = 2 است.

قطر گراف

بزرگ‌ترین خروج از مرکز رئوس گراف G را قطر گراف می‌نامند و آن را با (d(G نشان می‌دهند.

مثال

در گراف شکل زیر، d(G) = 3 است.

نقطه مرکزی

اگر خروج از مرکز یک رأس با شعاع آن برابر باشد، آن رأس را نقطه مرکزی می‌نامیم. به عبارت دیگر، اگر (e(V) = r(V باشد، V را نقطه مرکزی گراف G می‌نامیم.

مثال

در گراف شکل زیر، d نقطه مرکزی است، زیرا e(d) = r(d) = 2 است.

مرکز

مجموعه همه نقاط مرکزی یک گراف، مرکز آن نامیده می‌شود.

مثال

در گراف زیر، {d} مرکز گراف است.

محیط گراف

تعداد یال‌های طولانی‌ترین دور گراف G را محیط G می‌نامند.

مثال

در گراف شکل زیر، محیط برابر با ۶ است که از طولانی‌ترین دور a-c-f-g-e-b-a یا a-c-f-d-e-b-a به‌دست آمده است.

 

کمر گراف

تعداد یال‌های کوتاه‌ترین دور گراف را کمر گراف می‌نامیم و آن را با (g(G نمایش می‌دهیم.

در گراف شکل زیر، کمر برابر با ۴ است که از کوتاه‌ترین دور a-c-f-d-a یا d-f-g-e-d یا a-b-e-d-a به‌دست آمده است.

قضیه مجموع مرتبه‌های رئوس

اگر (G = (V, E یک گراف بدون جهت با رئوس {V = {V1, V2,…Vn باشد، آن‌گاه، داریم (|E| تعداد اعضای مجموعه E است):

$$\sum _{i=1}^{n}deg\left(V_i\right)=2|E|$$

نتیجه ۱

اگر (G = (V, E یک گراف جهت‌دار با رئوس {V = {V1, V2,…Vn باشد، آن‌گاه، داریم:

$$\sum _{i=1}^n{deg}^{+}\left(V_i\right)=|E|=\sum _{i=1}^n{deg}^{-}\left(V_i\right)$$

نتیجه ۲

در هر گراف بدون جهت، تعداد رئوس با مرتبه فرد، زوج است.

نتیجه ۳

در هر گراف بدون جهت، اگر مرتبه هر رأس را k در نظر بگیریم، آن‌گاه

|k|V| = 2|E

نتیجه 4

در هر گراف بدون جهت، اگر مرتبه هر رأس، حداقل برابر با k باشد، آن‌گاه داریم:

|k|V| ≤ 2|E

نتیجه ۵

در هر گراف بدون جهت، اگر مرتبه هر رأس، حداکثر برابر با k باشد، آن‌گاه داریم:

|k|V| ≥ 2|E

انواع گراف‌ها

گراف‌ها انواع مختلفی دارند که به تعداد رئوس، تعداد یال‌ها، اتصالات و ساختار کلی آن‌ها بستگی دارد. در این بخش، مهم‌ترین انواع گراف‌ها را معرفی خواهیم کرد.

گراف تهی

گرافی را که یال نداشته باشد، تهی یا پوچ می‌گوییم.

مثال

شکل زیر، گرافی را نشان می‌دهد که سه رأس به‌نام‌های «b» ،«a» و «c» دارد، اما یالی ندارد. به همین دلیل، این گراف را تهی می‌نامیم.

گراف بدیهی

گرافی که فقط یک رأس دارد، بدیهی نامیده می‌شود.

مثال

گراف شکل زیر که فقط یک رأس «a» دارد، گرافی بدیهی است.

گراف بدون جهت

گراف بدون جهت، گرافی است که یال دارد، اما یال‌های آن جهت ندارند.

مثال

در گراف شکل زیر «f» ،«e» ،«d» ،«c» ،«b» ،«a» و «g» رئوس و «gf» ،«ag» ،«da» ،«cd» ،«bc» ،«ab» و «ef» یال‌های گراف هستند. از آن‌جایی که گراف بدون جهت است، یال‌های «ab» و «ba»، یکسان هستند. این گفته برای سایر یال‌های گراف نیز صادق است.

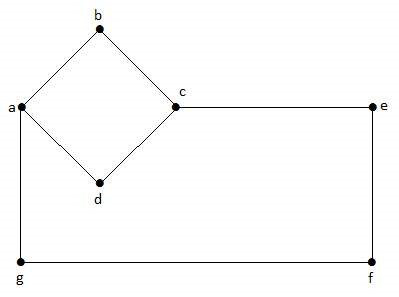
گراف جهت‌دار

در یک گراف جهت‌دار، هر یال دارای جهت است.

مثال

در گراف شکل زیر «f» ،«e» ،«d» ،«c» ،«b» ،«a» و «g» رئوس و «fe» ،«ec» ،«ad» ،«dc» ،«cb» ،«ab» و «gf» و «ga» یال‌های گراف هستند. از آن‌جایی که گراف جهت‌دار است،‌ جهت یال‌ها با فلش مشخص شده است. دقت کنید که در یک گراف جهت‌دار، «ab» با «ba» تفاوت دارد.

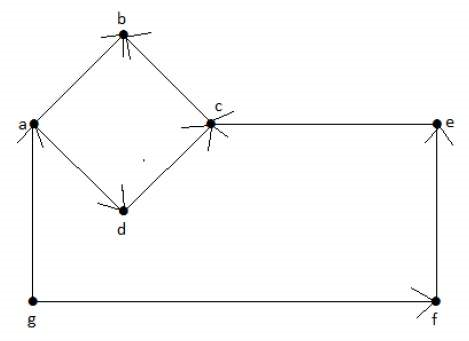
گراف ساده

گرافی را که حلقه و یال موازی نداشته باشد، یک گراف ساده می‌نامیم.

• حداکثر تعداد یال‌های ممکن در یک گراف ساده با n رأس، برابر با $$n_{C_2}=n(n-1)/2$$.
• تعداد گراف‌های ساده‌ای را که می‌توان با n رأس ساخت، برابر است با: $$2^{n_{C_2}}=2^{n(n-1)/2}$$.

مثال

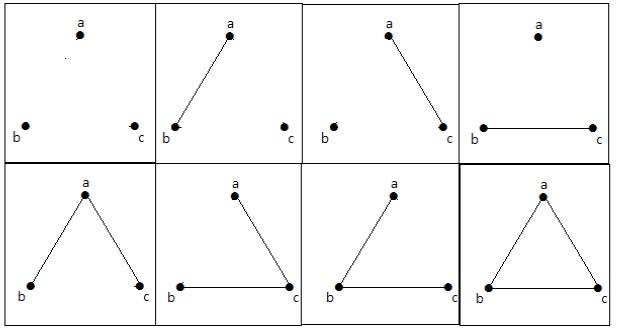
در گراف شکل زیر، سه رأس و سه یال وجود دارد که حداکثر تعداد ممکن است (البته به‌جز حلقه و یال موازی). حداکثر تعداد گراف‌های ساده‌ای که با سه رأس می‌توان ساخت، برابر با ۸ است. اثبات این گفته‌ها به سادگی با استفاده از فرمول‌های بالا امکان‌پذیر است.

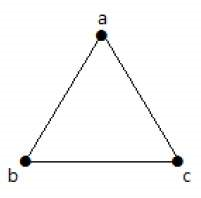
گراف‌های زیر، ۸ حالت ممکن را نشان می‌دهند.

گراف همبند

گراف G را همبند گوییم، اگر یک مسیر بین هر دو رأس آن وجود داشته باشد. در حقیقت، باید حداقل یک یال برای هر رأس وجود داشته باشد.

مثال

در گراف شکل زیر، برای هر رأس می‌توان مسیری پیدا کرد که به رأس دیگر برسد. بنابراین، گراف همبند است.

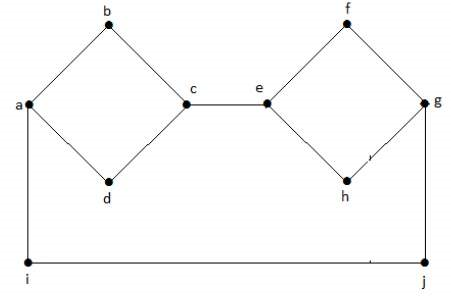
گراف ناهمبند

گراف G را ناهمبند گوییم، اگر حداقل دو رأس جدا داشته باشد.

مثال ۱

شکل زیر، یک گراف ناهمبند را نشان می‌دهد که دو بخش دارد؛ یکی شامل رئوس «c» ،«b» ،«a» و «d» و دیگری شامل رئوس «g» ،«f» ،«e» و «h».

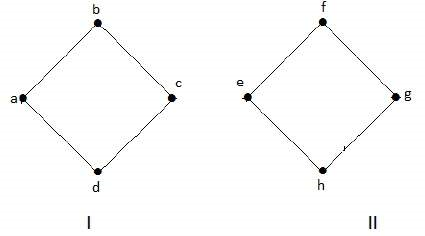
مثال ۲

شکل زیر، یک گراف ناهمبند را نشان می‌دهد که دو بخش a-b-f-e و c-d دارد.

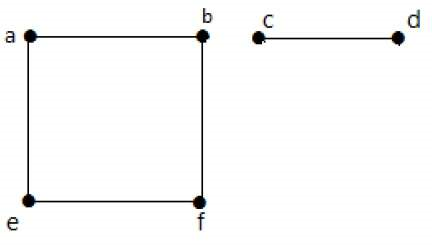
گراف منتظم

گرافی را منتظم می‌نامیم که همه رئوس آن، مرتبه یکسانی داشته باشند. اگر در یک گراف، درجه هر رأس، برابر با «k» باشد، آن گراف را گراف k-منتظم می‌گوییم.

مثال

در گراف‌های زیر، همه رئوس مرتبه یکسانی دارند. بنابراین، منتظم هستند.

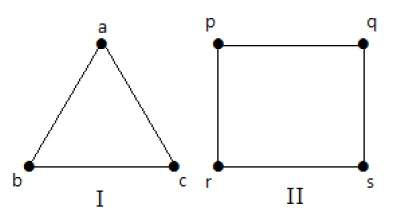
در هر دو گراف بالا، مرتبه رئوس برابر با ۲ است، بنابراین، این دو گراف، ۲-منتظم هستند.

گراف کامل

گراف ساده‌ای را کامل می‌گوییم که هریک از رأس‌های آن، با رئوس دیگر یک یال مشترک داشته باشد و آن را با $$K_n$$ نشان می‌دهیم.

مثال

در گراف‌های زیر، هر رأس جز خودش با سایر رئوس ارتباط دارد.

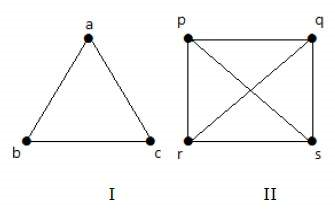
در گراف I داریم:

	a	b	c
a	متصل نیست	متصل است	متصل است
b	متصل است	متصل نیست	متصل است
c	متصل است	متصل است	متصل نیست

برای گراف II نیز می‌توان جدول زیر را ارائه کرد:

	p	q	r	s
p	متصل نیست	متصل است	متصل است	متصل است
q	متصل است	متصل نیست	متصل است	متصل است
r	متصل است	متصل است	متصل نیست	متصل است
s	متصل است	متصل است	متصل است	متصل نیست

گراف دوری

یک گراف ساده با n رأس و n یال (n >= 3)، یک گراف دوری نامیده می‌شود، اگر همه یال‌های آن، دوری به‌طول n را تشکیل دهند. به عبارت دیگر، اگر مرتبه هر رأس گراف، ۲ باشد، آن‌گاه گراف دوری است. گراف دوری را با $$C_n$$ نشان می‌دهند.

مثال

گراف‌های شکل زیر را در نظر بگیرید.

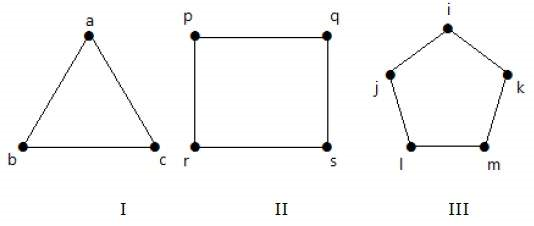
• گراف I سه رأس و سه یال دارد که دور ab-bc-ca را تشکیل می‌دهند.
• گراف II چهار رأس و چهار یال دارد که دور pq-qs-sr-rp را تشکیل می‌دهند.
• گراف III پنج رأس و پنج یال دارد که دور ik-km-ml-lj-ji را تشکیل می‌دهند.

بنابراین، همه گراف‌های بالا، گراف دوری هستند.

گراف چرخ

گراف چرخ، با افزدون یک رأس جدید به گراف دوری $$C_{n-1}$$ به‌دست می‌آید. گراف چرخ را با $$W_n$$ نشان می‌دهند. رأس جدید، هاب نامیده می‌شود.

مثال

سه گراف زیر، گراف چرخ هستند.

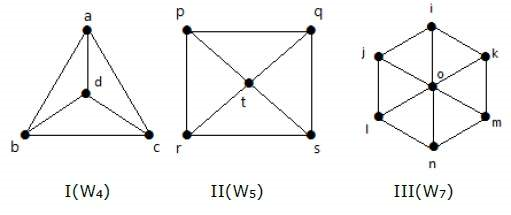
گراف مدوّر یا دوردار

گرافی را مدوّر یا دوردار گوییم که حداقل یک دور داشته باشد.

مثال

در گراف شکل زیر، دو دور a-b-c-d-a و c-f-g-e-c وجود دارد. بنابراین، گراف زیر یک گراف مدوّر یا دوردار است.

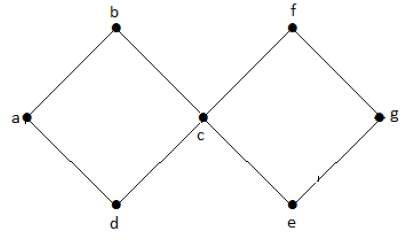
گراف غیرمدوّر

گرافی را که دوری نداشته باشد، گراف غیرمدور می‌نامیم.

مثال

در گراف شکل زیر، هیچ دوری وجود ندارد، بنابراین، گراف غیرمدور است.

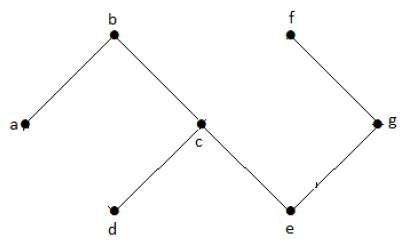
گراف دوبخشی

گراف ساده (G = (V, E را با دو افراز {V = {V1, V2 یک گراف دوبخشی می‌نامیم، اگر هر یال E به یک رأس از $$V_1$$ و یک رأس از $$V_{۲}$$ وصل باشد. در حالت کلی، یک گراف دوبخشی، دو مجموعه از رئوس ($$V_1$$ و $$V_2$$) است که هر یال از آن، رأسی از $$V_1$$ را به رأسی از $$V_2$$ وصل می‌کند.

مثال

در گراف شکل زیر، می‌توان دو مجموعه رأس $$V_{۱}$$ و $$V_2$$ را مشاهده کرد. در این‌جا، دو یال «ae» و «bd»‌، رئوس دو مجموعه را به یک‌دیگر وصل کرده‌اند.

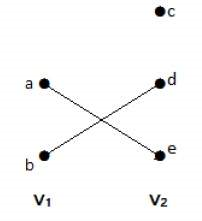
گراف دوبخشی کامل

گراف دوبخشی (G = (V, E را با افراز {V = {V1, V2 یک گراف دوبخشی کامل می‌گوییم، اگر همه رئوس $$V_{۱}$$ به همه رئوس $$V_{۲}$$ متصل باشند.

مثال

گراف شکل زیر، یک گراف دوبخشی کامل است، زیرا یال‌ها همه رئوس دو مجموعه $$V_{۱}$$ و $$V_{۲}$$ را به هم وصل می‌کنند.

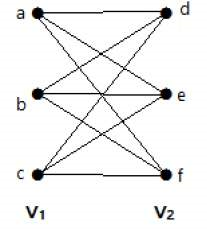
اگر V1| = m| و V2| = n| باشد، آن‌گاه گراف دوبخشی کامل با Km, n نشان داده می‌شود.

• Km, n، تعداد (m+n) رأس و (mn) یال دارد.
• اگر m=n باشد، Km, n یک گراف منتظم است.

توجه کنید که در حالت کلی،‌ گراف دوبخشی کامل، یک گراف کامل نیست. Km,n یک گراف کامل است، اگر m=n=1 باشد.

حداکثر تعداد یال‌های یک گراف دوبخشی با n رأس، از رابطه $$\left[\frac{n^2}{4}\right]$$ به‌دست می‌آید.

گراف ستاره

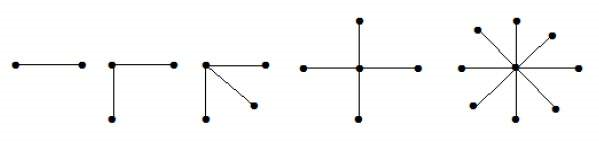
یک گراف دوبخشی کامل، به‌فرم K1, n-1 یک گراف ستاره با n رأس است. به عبارت دیگر، یک گراف دوبخشی کامل را گراف ستاره می‌گوییم، اگر یک رأس به یک مجموعه متعلق باشد و همه رئوس باقی‌مانده به سایر مجموعه‌ها تعلق داشته باشند.

مثال

هر یک از گراف‌های شکل زیر، n رأس دارند، که 1-n تا از رئوس آن‌ها به یک رأس متصل است.

مکمل گراف

گراف ساده $$\overline{G}$$ را مکمل گراف ساده $$G$$ می‌نامیم، اگر رئوس آن‌ها یکسان بوده و هر دورأسی که در $$G$$ مجاور نبوده‌اند، در $$\overline{G}$$ مجاور باشند.

ترکیب دو گراف مکمل، یک گراف کامل را تشکیل می‌دهد.

مثال

در شکل زیر، گراف I دو یال «cd» و «bd» دارد. گراف II مکمل این گراف است که ۴ یال دارد. همان‌طور که می‌بینیم، یال‌های گراف I در گراف II وجود ندارند و بالعکس.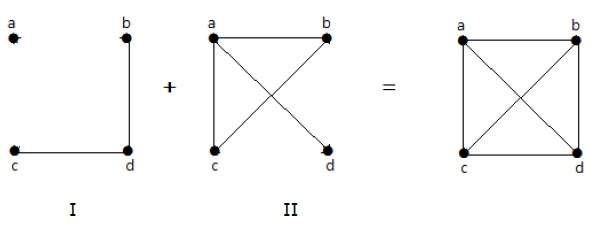

در شکل بالا، ترکیب دو گراف، یک گراف کامل را تشکیل داده است.

واژه‌نامه

واژه	معادل انگلیسی	واژه	معادل انگلیسی
گراف	Graph	قطر گراف	Diameter of a Graph
نقطه	Point	نقطه مرکزی	Central Point
خط	Line	محیط گراف	Circumference
رأس	Vertex	کمر گراف	Girth
یال	Edge	گراف تهی	Null Graph
حلقه	Loop	گراف بدیهی	Trivial Graph
مرتبه رأس	Degree of Vertex	گراف بدون جهت	Non-Directed Graph
رأس آویزان	Pendent Vertex	گراف جهت‌دار	Directed Graph
رأس جدا	Isolated Vertex	گراف ساده	Simple Graph
مجاورت	Adjacency	گراف همبند	Connected Graph
یال‌های موازی	Parallel Edges	گراف ناهمبند	Disconnected Graph
گراف چندگانه	Multi Graph	گراف منتظم	Regular Graph
دنباله مرتبه گراف	Degree Sequence of a Graph	گراف کامل	Complete Graph
فاصله بین دو رأس	Distance between Two Vertices	گراف دوری	Cycle Graph
خروج از مرکز یک رأس	Eccentricity of a Vertex	گراف چرخ	Wheel Graph
شعاع گراف	Radius	گراف مدوّر	Cyclic Graph
مرکز	Centre	گراف غیرمدوّر	Acyclic Graph
گراف دوبخشی	Bipartite Graph	گراف دوبخشی کامل	Complete Bipartite Graph
گراف ستاره	Star Graph	مکمل گراف	Complement of a Graph
دور	Circuit	مسیر	Path

در آموزش‌های آینده، درباره گراف اویلری و کات‌ست و درخت در گراف بحث خواهیم کرد. در صورتی که مباحث بیان شده برای شما مفید بوده و می‌خواهید درباره سایر موضوعات مربوط به ریاضیات، مطالب بیشتری یاد بگیرید، آموزش‌های زیر به شما پیشنهاد می‌شوند:

• گزاره ها و سورهای منطقی — به زبان ساده
• نمایش ماتریسی گراف — به زبان ساده
• اصل لانه کبوتر — به زبان ساده
• برهان خلف — به زبان ساده